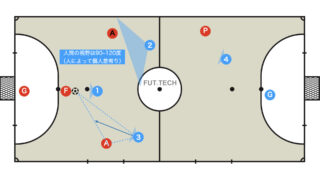
「あなたは普段何を考えてフットサルをしていますか?」
フットサルにおいてゴールから逆算する思考は非常に重要である。
しかし、ゴールから逆算するといっても抽象的すぎてどうアプローチすれば良いのかわからないひとがほとんどではないのでしょうか。
その一つのアプローチの仕方として「ゴールからの距離×角度」という考え方がある。
この記事では、円周角の定理(幾何学)を使って「ゴールからの距離×角度」を計算することで導かれるたった一つの客観的法則を示す。
この概念はセットプレーの定義や壁の枚数を考える上でも非常に重要な概念なため競技フットサルをプレーするにあたり必見である。
フィニッシュの基本原則
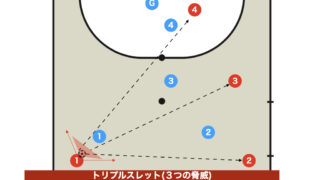
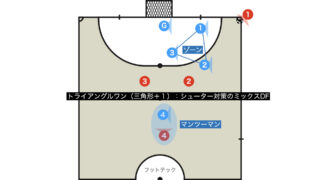
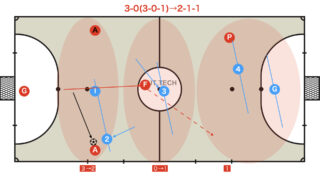
フィニッシュトライアングル(3角形+1、Y字)の形成
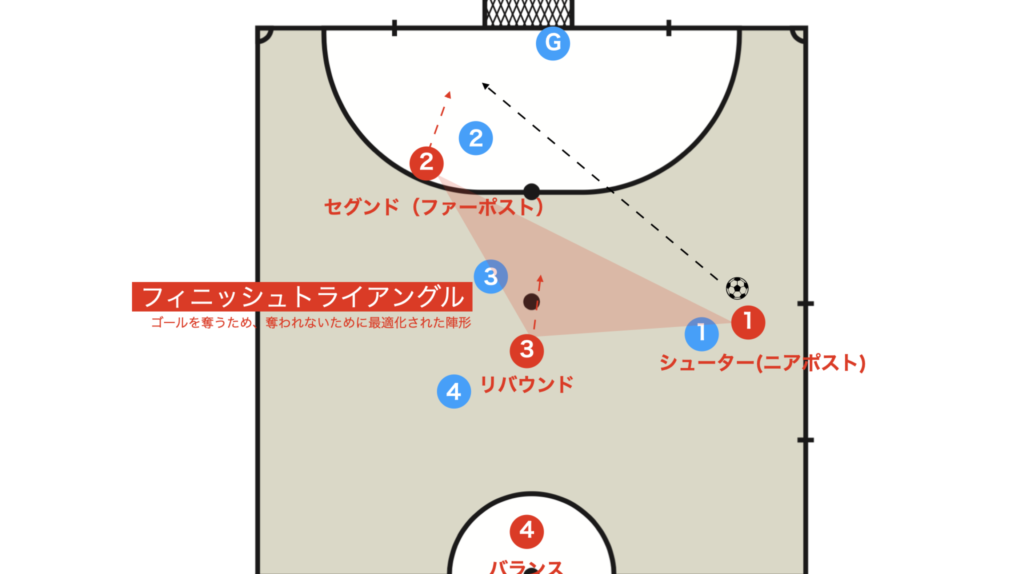
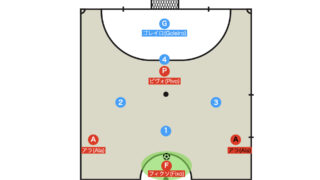
フィニッシュ時に「三角形(シューター、セグンド、リバウンド)+1(バランス)」の配置をつくることがゴールを奪うため、奪われないために最適化された陣形と言われている。
この陣形はフィニッシュトライアングルと呼ばれ、各選手の役割は以下のとおりである。
- シューター:シュートあるいはセグンドへパス(場合によってはリバウンドと兼任)
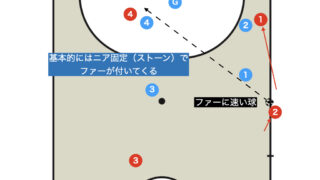
- セグンド:ファー詰め
- リバウンド:こぼれ球の回収、被カウンター対応
- バランス:最終ラインでのカバーリング、指示
この理論は幾何学的にも自分たちのスペースを最大化出来るものとして証明できる揺るぎのない理論である。
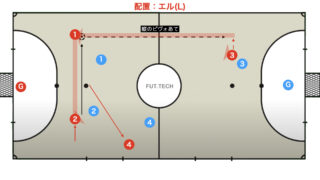
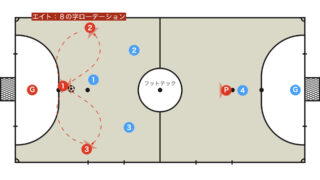
ゲーゲンプレス(即時、カウンタープレス)
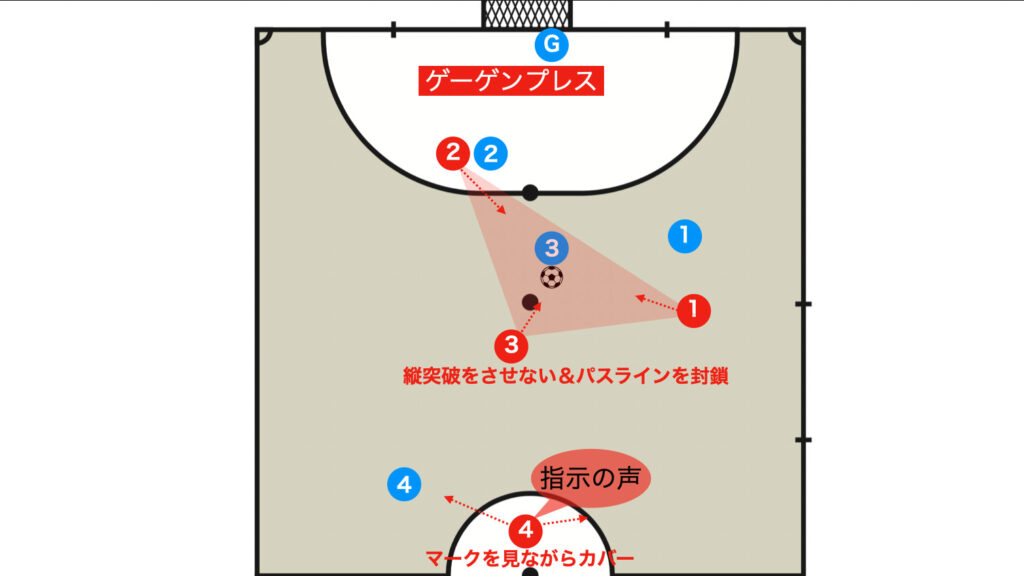
クロップ監督率いるリバプールでお馴染み、ボールを失った後、すぐに奪い返すためのプレスをかけるゲーゲンプレッシングという戦術がある。
ゲーゲンプレスについての詳しい解説は割愛するが、フィニッシュトライアングルはゲーゲンプレスをかける上でも最適な陣形と言える。
円周角の定理
ゴールからの角度を算出するために中学校の数学で習う円周角の定理を最初におさらいする。
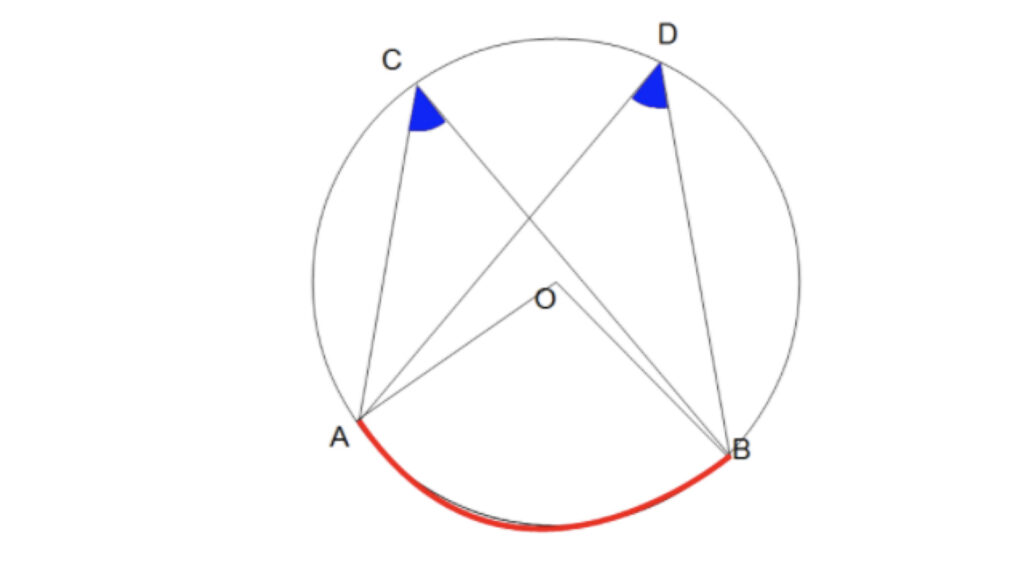
弧ABに対する円周角の大きさはつねに一定であり、
その角の大きさは、その弧に対する中心角の大きさの半分である。
- ∠ACB=∠ADB
- ∠AOB=2∠ACB=2∠ADB
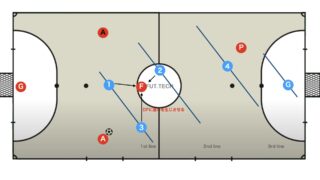
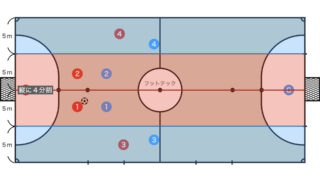
円周角の定理のフットサルコートへの適用
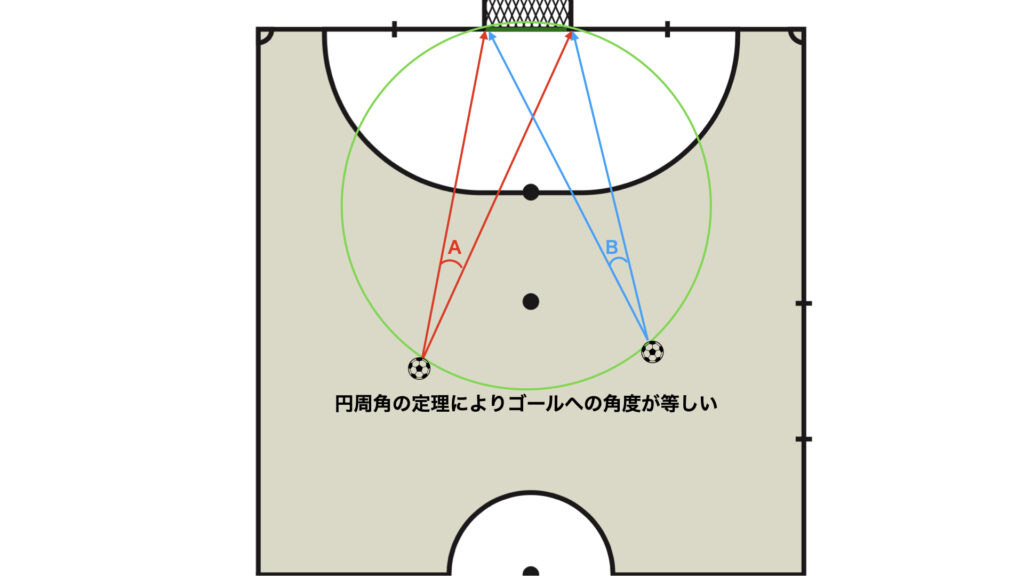
上図のようにフットサルコートのゴールを起点に円を書いて円周角の定理を適用させると
角Aと角Bの角度が等しくなる。
最後まで記事を読んでいただき誠にありがとうございます。
↑にSNSシェアボタンがございますのでこの記事が有益だと思った方はシェアして頂けると幸いです。
Twitterでフットサルの戦術に関する有益な情報を発信していますのでまだフォローしていない方はフォローお願いします!
私達は日本のフットサルの競技レベルを上げるためにFリーグや海外での指導経験のある方との意見交換を通じて良質な情報を発信しています。
何か分からない点、間違っている箇所がございましたら↓のコメント蘭からお気軽にコメントください。
定期的に記事更新していますので今後も読みたいと思った方はブックマークの登録 or 「フットテック」で検索していただけると幸いです。